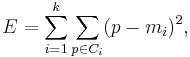CURE data clustering algorithm

CURE (Clustering Using REpresentatives) is an efficient data clustering algorithm for large databases that is more robust to outliers and identifies clusters having non-spherical shapes and wide variances in size.

Contents

Drawbacks of traditional algorithms

With the partitional clustering algorithms, which for example use the sum of squared errors criterion

E = \sum_{i=1}^{k} \sum_{p \in C_i} (p-m_i)^{2},

when there are large differences in sizes or geometries of different clusters, the square error method could split the large clusters to minimize the square error which is not always correct. Also, with hierarchic clustering algorithms these problems exist as none of the distance measures between clusters (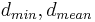d_{min}, d_{mean}) tend to work with different shapes of clusters. Also the running time is high when n is very large. The problem with the BIRCH algorithm is that once the clusters are generated after step 3, it uses centroids of the clusters and assign each data point to the cluster with closest centroid. Using only the centroid to redistribute the data has problems when clusters do not have uniform sizes and shapes.

CURE clustering algorithm

To avoid the problems with non-uniform sized or shaped clusters, CURE employs a novel hierarchical clustering algorithm that adopts a middle ground between the centroid based and all point extremes. In CURE, a constant number c of well scattered points of a cluster are chosen and they are shrunk towards the centroid of the cluster by a fraction α. The scattered points after shrinking are used as representatives of the cluster. The clusters with the closest pair of representatives are the clusters that are merged at each step of CURE's hierarchical clustering algorithm. This enables CURE to correctly identify the clusters and makes it less sensitive to outliers.

The algorithm is given below.

The running time of the algorithm is O(n2 log n) and space complexity is O(n).

The algorithm cannot be directly applied to large databases. So for this purpose we do the following enhancements

Pseudocode

CURE(no. of points,k)

Input : A set of points S

Output : k clusters

  1. For every cluster u (each input point), in u.mean and u.rep store the mean of the points in the cluster and a set of c representative points of the cluster (initially c = 1 since each cluster has one data point). Also u.closest stores the cluster closest to u.
  2. All the input points are inserted into a k-d tree T
  3. Treat each input point as separate cluster, compute u.closest for each u and then insert each cluster into the heap Q. (clusters are arranged in increasing order of distances between u and u.closest).
  4. While size(Q) > k
  5. Remove the top elemnt of Q(say u) and merge it with its closest cluster u.closest(say v) and compute
  6. the new representative points for the merged cluster w. Also remove u and v from T and Q.
  7. Also for all the clusters x in Q, update x.closest and relocate x
  8. insert w into Q
  9. repeat

References